9. Sınıf Matematik Açıortay Konu Anlatımı pdf dersimize hoşgeldiniz arkadaşlar. Bu dersimizde sizlere üçgenin yardımcı elemanlarından olan açıortaydan bahsedeceğiz.

ÜÇGENİN YARDIMCI ELEMANLARI

 
Üçgenin açıortayı, kenarortayı ve yüksekliği üçgenin yardımcı elemanlarıdır.

ÜÇGENDE AÇIORTAY

Bir açıyı iki eş açıya ayıran ışına açıortay denir. m(AOB)  = m(BOC) ise [OB, AOC açısının açıortayıdır.

Verilen bir açı cetvel ve pergel kullanılarak şu şekilde iki eş açıya ayrılabilir.
I. Adım
Cetvel yardımıyla AOB açısı çiziniz.

II. Adım
AOB açısının O noktasına pergelin sivri ucunu koyarak O merkezli bir çember çember yayı çiziniz. Bu çember yayının açının kollarını kestiği noktalar K ve N olsun.

III. Adım
Pergelin sivri ucunu K noktasına koyarak yarıçapı [OK] olan bir çember çizilir. Aynı şekilde pergelin sivri ucunu N noktasına koyarak yarıçapı [ON] olan bir çember çizilir. |OK| = |ON| dir. Bu çemberlerin kesiştiği noktalardan birisi P olsun.

IV. Adım
Son olarak O ve P noktaları birleştirildiğinde elde edilen [OP, AOB açısının açıortayıdır.

Açıortayın Özellikleri 

♦  Bir açıortay üzerinde alınan herhangi bir noktadan açının kollarına indirilen dikmelerin uzunlukları eşittir.  O hâlde |NC| = |ND| ve |OC| = |OD| dir.

Elde edilen üçgenlerin ortak doğru parçası, [ON] olduğundan A.K.A. eşlik teoreminden;
​\( \displaystyle\stackrel{Δ}{NCO}~ ≅ ~\displaystyle\stackrel{Δ}{NDO} \)​ olur.
 
♦  Bir üçgende iki iç açıortayın oluşturduğu açının ölçüsü, 90° den diğer köşedeki açının ölçüsünün yarısı kadar fazladır. ABC üçgeninde [BD] ve [DC] açıortaylar olmak üzere

​\( m(BDC) = 90 ~+ \displaystyle\frac{m(BAC)}{2} \)​ olur.
 
♦  ABC üçgeninde B ve C köşelerine ait dış açıortayların üçgeninde dışında olan bir  D noktasında kesişmeleriyle oluşan BDC açısının ölçüsü;

​\( m(BDC) = 90~ – \displaystyle\frac{m(BAC)}{2} \)​ olur.
 
♦  Bir üçgende bir iç açıortay ile bir dış açıortayın oluşturduğu açının ölçüsü diğer köşedeki açının ölçüsünün yarısına eşittir.
ABC üçgeninde [BD] iç açıortay, [CD] dış açıortay olmak üzere;

​\( m(BDC) = \displaystyle\frac{m(BAC)}{2} \)​ olur.
 
♦  İkizkenar bir üçgende tepe açısından tabana çizilen açıortay aynı zamanda yükseklik ve kenarortaydır.

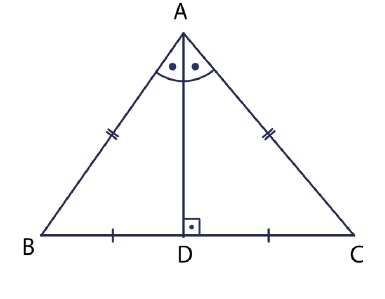
[AD] ⊥ [BC] ve  |BD| = |DC| olur.
 
Örnek;

m(BTN) = m(ATN),  [KL] = [TA,   [KM] = [TB,   [PR] = [TA,   [PS] = [TB ve
|KL| = 3x – 16, |KM| = 2x – 9, |PS| = x – 4 olduğuna göre |TR|/|RL| oranını bulunuz.
 
Çözüm;
Açıortay üzerindeki bir noktadan kenarlara indirilen dikmelerin uzunlukları eşittir. Buna göre |KL| = |KM|  olur. O da;
3x – 16  =  2x – 9 ise x = 7 olur. Bu durumda |PR| = |PS| = x -4 ve |KL| = |KM| = 3x – 16 ise;
|PR| = |PS| = 3 ve |KL| = |KM| = 5 olarak bulunur.

\( \displaystyle\stackrel{Δ}{TRP}~ ≅ ~\displaystyle\stackrel{Δ}{TLK} \)  olduğundan;
​\( \displaystyle\frac{|PR|}{|KL|} = \displaystyle\frac{|TR|}{|TL|} = \displaystyle\frac{3}{5} \)​ olur.
O halde ​\( \displaystyle\frac{|TR|}{|RL|} = \displaystyle\frac{3}{2} \)​ olur.
 
Örnek;
ABC üçgeninde, [BD] iç açıortay, [CD] dış açıortay, m(BDC) = 45º, |BC| = 10 cm, |EC| = 5 cm olduğuna göre |BE| = x değerinin kaç cm olduğunu bulunuz.

Çözüm;
m(CBE) = a ise m(DCP) = m(DCE) = 45 + a olur.
m(A)+ 2a = 90º + 2a ⇒ m(A) = 90º olur.
ABC üçgeninde [BE] iç açıortay olduğundan iç açıortay teoremi kullanılırsa;
​\( \displaystyle\frac{|AE|}{|AB|} = \displaystyle\frac{5}{10} \)​ olduğundan      |AE| = k ise |AB| = 2k olur.

1. Üçgende İç Açıortay

 
Bir üçgenin bir iç açısını iki eş açıya ayıran doğru parçasına o üçgenin iç açıortayı denir. Bir üçgende iç açıortaylar tek noktada kesişir. Kesiştikleri bu nokta üçgenin iç teğet çemberinin merkezidir.

[AS], A açısına ait açıortay olmak üzere |AS| = ​\( n_a \)​
[BR], B açısına ait açıortay olmak üzere |BR| = \( n_b \)​
[CP], C açısına ait açıortay olmak üzere |CP| = \( n_c \)​ ile gösterilir.
I noktası, iç açıortayların kesişim noktasıdır.

I noktası iç açıortayların kesişim noktası ve üçgenin iç teğet çemberinin merkezdir. D, E, F noktaları çemberin üçgene teğet noktaları olmak üzere;|IE| = |ID| = |IF| = r iç teğet çemberinin yarıçapıdır.
|AD| = |AE|
|BD| = |BF|
|CF| = |CE| olur.
 
Örnek;
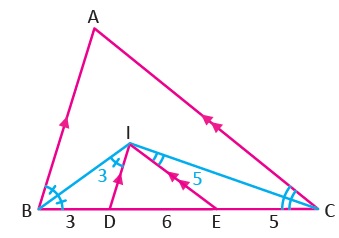
ABC üçgeninde, I noktası üçgenin iç teğet çemberinin merkezidir. [ID] // [AB], [IE] // [AC],  |BD| =  3 cm,  |DE| = 6 cm,  |EC| = 5 cm olduğuna göre IDE üçgeninin çevresinin kaç cm olduğunu bulunuz.

Çözüm;
I noktası üçgenin iç açıortaylarının kesişim noktasıdır. O hâlde [IB] ve [IC] iç açıortaylardır.
|ID| = |BD| = 3 cm, |IE| = |EC| = 5 cm dir. Bu durumda ​\( \displaystyle\stackrel{Δ}{Ç(IDE)} \)= 14​cm olarak bulunur.

2. Üçgende İç Açıortay Teoremi

 
♦  ABC üçgeninde, A açısına ait açıortay doğrusunun [BC] nı kestiği nokta N olsun.
|AB| = c, |AC| = b, |BN| = m, |NC| = n olmak üzere;
​\( \displaystyle\frac{c}{b} = \displaystyle\frac{m}{n} \)​ dir.

♦  ABC üçgeninde [AN] iç açıortay ve |AN| = x olsun. |AB| = c, |AC| = b, |BN| = m, |NC| = n olmak üzere;
​\( \displaystyle{x^2 = b.c – m.n} \)​ dir.
 
Örnek;
ABC üçgeninde, m(BAC) = 2. m(CBA), |BC| = 9 cm, |AC| = 6 cm olduğuna göre |AB| değerinin kaç cm olduğunu bulunuz.

Çözüm;
Soruda verilenlere göre, m(ABC) = α denirse m(BAC) = 2α olur.
[AN], BAC açısının açıortayı olmak üzere |BN| = x, |AB| = y ise bu durumda üçgende iç açıortay teoreminden;
x² = 6y – x(9-x)
x² = 6y – 9x + x²
6y = 9x
​\( \displaystyle\frac{y}{x} = \displaystyle\frac{3}{2} \)​olur. (1)
|AN| = x ve |NC| = 9 – x ise burada üçgende iç açıortay teoreminden;
​\( \displaystyle\frac{y}{6} = \displaystyle\frac{x}{9-x} ⇒ \displaystyle\frac{y}{x} = \displaystyle\frac{6}{9-x} \)​olur. (2)
|AB| = y değerini bulmak için bu iki eşitliği kullanırsak;
​\( \displaystyle\frac{3}{2} = \displaystyle\frac{6}{9-x} \)​
27 – 3x = 12
3x = 15
x = 5
y = |AB| = 7,5 cm olarak bulunur.
 

3. Üçgende Dış Açıortay

 
♦  Bir üçgenin bir dış açısını iki eş açıya ayıran ışına o üçgenin dış açıortayı denir. 
ABC üçgeninde ACP dış açısının açıortayı olan [CK, C açısına ait dış açıortaydır.

♦  Bir üçgende iki dış açıortay ile üçüncü açının iç açıortayı tek noktada kesişir(\( \displaystyle{I_A} \)​). Bu nokta, üçgenin dış teğet çemberinin merkezidir. 

A açısına ait dış teğet çemberinin yarıçapı \( \displaystyle{r_A} \) dır. D, E ve F noktaları çemberin değme noktaları olmak üzere \( \displaystyle{|I_AD|=r_A} \)olur.
 

4. Üçgende Dış Açıortay Teoremi

 
♦  ABC üçgeninde [AK] dış açıortay, K ∈ [BC, |AB| = c, |AC| = b olmak üzere;
​\( \displaystyle\frac{|KC|}{|KB|} = \displaystyle\frac{b}{c} \)​ olur.

♦  ABC üçgeninde [AK] dış açıortay, |AK| = y olsun. |AB| = c, |AC| = b olmak üzere;
y² = |KC|.|KB| – b.c ‘dir.
 
Örnek;

ABC üçgeninde [AK] iç açıortay, [AN] dış açıortay, |AB| = 8 cm, |AC| = 6 cm, |BC| = 7 cm olduğuna göre |KN| değerinin kaç cm olduğunu bulunuz.
Çözüm;

İç açıortay teoreminden;
​\( \displaystyle\frac{|AB|}{|AC|} = \displaystyle\frac{4}{3} = \displaystyle\frac{|BK|}{|KC|} \)​
olduğundan |BK| = 4k ise |KC| = 3k bulunur.
|BC| = 4k + 3k = 7k = 7 olduğundan k = 1 bulunur.
O halde |BK| = 4 cm ve |KC| = 3 cm olur. |CN| = x olsun. Dış açıortay teoreminden;
​\( \displaystyle\frac{x}{x+7} = \displaystyle\frac{6}{8} = \displaystyle\frac{3}{4} \)​⇒ 4x = 3x + 21 ⇒ x = 21 olur. Bu durumda |KN| = 3k + x = 3 + 21 = 24 cm olarak bulunur.
 
Açıortay konumuz burada bitti arkadaşlar. Konuyla ilgili daha fazla örnek soru görmek için aşağıdaki linklere tıklayabilirsiniz.
Çözümlü Açıortay Soruları – 1
Çözümlü Açıortay Soruları – 2
Sorularda kullanacağınız pratik formüller için ise aşağıdaki yazımıza göz atabilirsiniz. 🙂 Derslerinizde başarılar diliyoruz.
Üçgende Açıortay Bağıntıları Özellikleri Formülleri