Fonksiyon Nedir? Fonksiyon Ne işe yarar, Fonksiyon Tanımı, Fonksiyon Nedir Örnekler, Fonkiyon Çeşitleri
Fonksiyon Kavramı
* Boş olmayan iki kümeden biri olan A kümesinin her bir elemanını B kümesinin bir ve yalnız bir elemanına eşleyen ilişkiye A dan B ye tanımlı fonksiyon denir. Fonksiyonlar genellikle f harfiyle gösterilir.
• A ve B boş olmayan iki küme olmak üzere f, A dan B ye tanımlı bir fonksiyon ise;
i. A nın her bir elemanı, B nin yalnız bir elemanı ile eşlenir.
ii. A da eşlenmeyen eleman yoktur.
• Bir A kümesinden B kümesine tanımlı f fonksiyonu kısaca
f : A → B, x → y = f ( x ) şeklinde gösterilir. Burada A ya fonksiyonun tanım kümesi, B ye ise fonksiyonun değer kümesi denir. A nın eşlendiği f ( A ) kümesine de görüntü kümesi denir.

Şimdi bu durum ile ilgili örnek yapıp konuyu daha iyi anlamaya çalışalım.
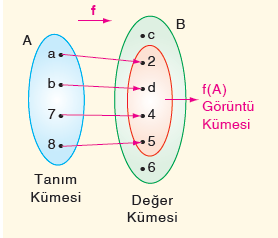
Örnek: Aşağıda verilen f fonksiyonunu, f fonksiyonunun tanım, görüntü
ve değer kümesini liste biçiminde yazalım.
Cevap:
a. f fonksiyonunun tanım kümesi, A = { a, b, 7, 8 } dir.
b. f fonksiyonunun değer kümesi, B = { c, 2, d, 4, 5, 6 } dır.
c. f fonksiyonunun görüntü kümesi, f ( A ) = { 2, d, 4, 5 } tir.
Fonksiyon Türleri
Tanım kümesinin farklı alt aralıklarında kuralı değişiklik gösteren fonksiyonlara parçalı fonksiyon denir.

Parçalı Fonksiyon örnek soru ve çözümü

A boş kümeden farklı bir küme olmak üzere A dan A ya ( A da ) tanımlı, her elemanı kendine eşleyen fonksiyona birim ( özdeşlik ) fonksiyon denir. Birim fonksiyonu genel olarak
I : A → A , I ( x ) = x veya I : x → x şeklinde gösterilir.
Birim Fonksiyon Örnek Soru ve çözümü
Soru: Tam sayılar kümesinde tanımlı f ( x ) = ( 2a – 3 ) x + b + 2 fonksiyonu birim
fonksiyondur. Buna göre a + b toplamını bulalım.
Cevap: Birim fonksiyonunun kuralında x in katsayısı 1, sabit terimi ise 0 dır.

f : A → B fonksiyonunda, A kümesinin bütün elemanları B kümesinin yalnız bir elemanı ile eşleniyorsa f fonksiyonuna sabit fonksiyon denir.
Sabit Fonksiyon Örnek Soru ve çözümü
Soru: f ( x ) = 4x + ( m + 2 ) x + 3 fonksiyonunun sabit fonksiyon olması için
m nin değerini bulalım.
Cevap: ( x ) = 4x + ( m + 2 ) x + 3 fonksiyonunun sabit fonksiyon olması için x li terim içermemelidir. Bu durumda 4x + ( m + 2 ) x = 0 ⇒ m + 2 = – 4
⇒ m = – 6 bulunur.
f : R → R ve a , b ∈ R olmak üzere f ( x ) = ax + b kuralı ile verilen fonksiyonlara doğrusal fonksiyon denir.
Doğrusal Fonksiyon Örnek Soru ve çözümü
Soru: Gerçek sayılarda tanımlı f doğrusal fonksiyonu için f ( 1 ) = 4 ve f ( 2 ) = 7 dir. Buna göre f fonksiyonunun kuralını bulup fonksiyonun grafiğini çizelim.
Cevap: f doğrusal ise f ( x ) = ax + b ( a, b ∈ R ) dir.
f ( 1 ) = 4 ⇒ a . 1 + b = 4 ⇒ a + b = 4 … ( I )
f ( 2 ) = 7 ⇒ a . 2 + b = 7 ⇒ 2a + b = 7 … ( II )


Bire Bir, Örten ve İçine Fonksiyon

Yukarıdaki durum sağlanıyorsa f fonksiyonu bire bir ( 1 – 1 ) fonksiyondur.
• f : A → B fonksiyonunda her y ∈ B için f ( x ) = y olacak biçimde en az bir x ∈ A varsa f fonksiyonu örten fonksiyondur, yani f ( A ) = B ise f fonksiyonu örtendir.
• f : A → B fonksiyonu için f ( A ) ≠ B ise yani değer kümesinde eşlenmeyen en az bir eleman kalıyorsa f fonksiyonu içine fonksiyondur.
Örnek: f : R → R , f ( x ) = x + 2 fonksiyonunun bire bir ve örtenlik durumlarını
inceleyelim.
Cevap: 
Tek ve Çift Fonksiyonlar
A simetrik bir küme olmak üzere f : A → R bir fonksiyon olsun. Her x ∈ A için;
• f ( –x ) = f ( x ) ise f çift fonksiyondur.
• f ( –x ) = –f ( x ) ise f tek fonksiyondur.
Örnek: Gerçek sayılarda tanımlı aşağıdaki fonksiyonların tek ya da çift olup
olmama durumlarını inceleyelim.
Cevap: 