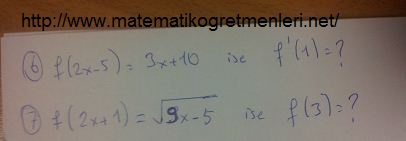Matematikte fonksiyon konusu ile ilgili okul derslerine ve sınavlara hazırlanan öğrencilere faydalı olması için hazırlamış olduğumuz 10 adet çözümlü soru testimizi aşağıda sizinle paylaşıyoruz.

ÇÖZÜM 1 : f(x) fonksiyonunda x gördüğümüz yere -1 ve -3 değerlerini vererek toplama işlemini yapacağız;
f(-1) = 3.(-1) – |-1+2| = -3 – (1) = -4
f(-3) = 3.(-3) – |-3+2| = -9 – (1) = -10 olur
f(-1) + f(-3) = -4 + -10 = -14 olur sonuç
ÇÖZÜM 2 : f(x) doğrusal fonksiyonunu ax+b şeklinde düşünelim. Hem f(2) hemde f(4) ü yerine yazıp a ve b değerlerini bulalım.
f(2) = 2a + b = 3
f(4) = 4a + b = 6
denklem sistemini taraf tarafa çıkarma işlemi yaparak çözersek a = 3/2 b = 0 çıkar. Buradan f(x) fonksiyonum;
f(x) 3/2x + 0 dan f(6) için (3/2).6 + 0 dan sonuç 9 olur.
Çözüm 3: Soruda f(4) = 2 verildiğine göre x yerin 3 yazalım;
f(3) = 2.3 + 1 – f(4) olur buradan f(3) = 5 buluruz.
x yerine bu sefer 2 yazalım;
f(2) = 2.2 +1 – f(3) olur ve f(2) = 0 değerini buluruz.
Çözüm 4 : x yerine 2 yazarsak fonksiyonun içindeki ifade 3 olur. O halde;
f(4-1) = 3.4 + 4.2 – 5 ten f(3) = 15 olur.
Çözüm 5 : Soruda fonksiyonun sabit fonksiyon olduğu verilmiş. O halde x in katsayı ile sabit sayıların oranı birbirine eşit olmalı. yani;
3 / 1 = b / 2 olmalı ki b buradan b = 6 bulunur.
Çözüm 6 : Tersi için f(3x+10) = 2x -5 şeklinde düşünüp fonksiyonun içini 1 e eşitlemek gerekli.
3x + 10 = 1 için x = -3 yani x gördüğümüz yerede -3 yazacağız. O halde;
f(3.(-3)+10) = 2.(-3) – 5 ten sonuç -11 olur.
Çözüm 7 : Önceki sorudaki gibi fonksiyonun için 3 e eşitleyeceğiz.
2x + 1 = 3 için x e 1 değeri vermemiz gerekli.
x = 1 için => f(1) = kök içinde 4 ten sonuç 2 olur.
Çözüm 8 : İlk öncelikle bileşke fonksiyonda içteki f(2) değerini bulmamız gerekli.
f(2) = 4 olur.
Şimdi ise g(4) ü bulalım;
g(4) = 2.4 – 1 = 7
Çözüm 9 : Sırası ile tüm sonuçları bulalım.
x = -1 için => f(-1) = |-1-2| – |-1| = 2
x = 0 için => f(0) = |0-2| – |0| = 2
x = 1 için => f(1) |1-2| – |1| = 0 olur .
Sonuç : 2 + 2 + 0 = 4 tür.
Çözüm 10 : Fonksiyonun içininin 3 olması için x’e -2 değeri vermemiz gerekli.
x = -1 için f(3) = 4 – (-2) + 2 den f(3) = 8 olur.
Soru: Aşağıdaki g fonksiyonları sabit fonksiyonlardır. Buna göre her bir seçenekteki g ( m ) değerlerini bulunuz.
a. g ( x ) = ( m + 2 ) x + m + 1
b. g ( x ) = 4x – ( m + 1 ) x – m
c. g ( x ) = ( m + 3 ) x + 5
Cevap: Sabit fonksiyon olduğuna göre x terimli bir ifade olmamalı. Bu nedenle de x terimlerini yok etmemiz için başlarındaki katsayıyı 0 yapmalıyız.
a şıkkındaki g ( x ) = ( m + 2 ) x + m + 1 fonksiyonunda ( m + 2 ) buranın 0 a eşit olması gerek. Bu nedenle de m=-2 olur.
m yerine -2 değerini koyarsakta g(-2) = ( -2 + 2 ) x – 2 + 1 = -1 olarak buluruz.
b şıkkında ise g ( x ) = 4x – ( m + 1 ) x – m fonksiyonunda 4 -m -1 = 0 olmalı
Buradan da m = 3 oalrak buluruz.
m değerini yerine koyarsak g(x) = – m den g(3) = -3 olur.
c şıkkında ise g ( x ) = ( m + 3 ) x + 5 fonksiyonunda (m + 3) = 0 olmalı ve buradan da m = -3 olur.
m değerini yerine koyarsak g(x) = 5, g(-3) = 5 olarak buluruz.
Soru: Birikmiş 100 TL parasından her gün 5 TL para harcayan Bülent’in günlere ( x ) göre kalan parasını ( y ) veren y = f ( x ) fonksiyonunu bulup tanım ve görüntü kümelerini belirleyip grafiğini çiziniz.
Cevap: y=f(x) = 100 – 5x olur.
x: gün
x = 0 için y = 100
x = 1 için y = 95
.
.
.
x = 20 için y = 0
f : [0,20] buradan da [0,100] olur
Grafiğini çizecek olursak ta

Soru: Dikildiğinde 20 cm boyunda olan bir fidan her ay 2 cm uzamaktadır. Fidanın aylara ( x ) göre boyunu ( y ) veren y = f ( x ) fonksiyonunu bulup tanım ve görüntü kümelerini belirtip grafiğini çiziniz.
Cevap: Yanıtı aşağıdaki grafik ve açıklamalarda bulabilirsiniz arkadaşlar.

Soru: f ( x ) doğrusal fonksiyonunda f ( 2 ) = 5 ve f ( – 1 ) = – 1 olduğuna göre f ( 5 ) kaçtır?
Cevap: f(2) = 5 ise 2.2 + 1 = 5 şeklinde olabilir
f(-1) = -1 ise 2.(-1) + 1 = -1 olabilir
Yukarıdaki her iki fonksiyonda görüleceği üzere
f(x) fonksiyonumuz 2x + 1 olur. O halde
f(5) = 2.5 + 1 = 11 olur.
Soru: f : R→ R, f ( x ) = ( 2a – 4 )x 3+ ( b + 4 )x 2+ ( 4b – 8 ) x – 3a – b + 1 fonksiyonu çift fonksiyondur. Buna göre f ( 1 ) in değerini bulunuz.
Cevap: Çift fonksiyon olduğuna göre tek dereceli terimler olmamalı arkadaşlar.
Bu nedenle de;
2a – 4 = 0 dan a = 2
4b – 8 = 0 dan b=2 olur.
f(x) = 6x 2 – 7 den
f(1) = 6-7= -1 olarak buluruz.
Soru: Gerçek sayılarda tanımlı f ve h fonksiyonları için
f ( x ) = – x + 5 ve
( 3h – f ) ( x ) = 10 x – 2
olduğuna göre h ( 3 ) aşağıdakilerden hangisidir?
Cevap: f(x) fonksiyonunda f(3) = -3 + 5 = 2 olur.
(3h-f).(x) = 3.h(x) – f(x) = 10x -2 olur
x=3 için 3.h(3) – f(3) = 10.3 -2
3.h(3) – 2 = 28
3.h(3) = 30
h(3) =10 olarak buluruz.