İkinci Dereceden Denklem Formülleri ile ilgili hem bir bilinmeyenli hem de 2 bilinmeyenli tüm formülleri pdf formatında çözmmlü örnek sorular ile birlikte paylaşacağız sevgili öğrenciler.
ax² + bx + c = 0 Biçimindeki Denklemlerin Genel Çözümü
a ≠ 0 için ax² + bx + c = 0 denkleminin kökleri aşağıdaki formül ile bulunabilir. Burada b² – 4ac ifadesine denklemin diskriminantı denir ve Δ ile gösterilir.
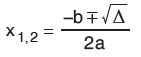
Örnek: x² + 6x + 9 = 0 denklemlerinin çözüm kümelerini diskriminant kullanarak bulalım
x² + 6x + 9 = 0 denkleminde, a = 1 , b = 6 ve c = 9 dur.
Δ = b² – 4ac ⇒ Δ = 6² – 4.1.9
= 36 – 36 dan = 0 dır.
Denklemin x1 = x2 = –3 şeklinde eşit iki kökü vardır.
İkinci Dereceden Bir Bilinmeyenli Denklemlerde Köklerin Varlığı
a ≠ 0 için ax² + bx + c = 0 denkleminde Δ = b² – 4ac olmak üzere;
- Δ > 0 ise denklemin birbirinden farklı iki gerçek kökü vardır. Bu kökler;
dir.
- Δ =0 ise denklemin eşit iki gerçek kökü ( çakışık iki kökü veya iki katlı kökü ) vardır. Bu kökler; x1 = x2 = -b/2a dır.
- Δ< 0 ise denklemin gerçek kökü yoktur. Başka bir deyişle, bu denklemin gerçek sayılarda çözüm kümesi boş kümedir.
Örnek: Aşağıda verilen denklemlerin köklerinin varlığını inceleyelim.
a. x² + 6 x + 11 = 0 b. x² – 13x – 3 = 0 c. 4 x² + 12 x + 9 = 0
a) x² + 6 x + 11 = 0 denklemii için Δ = b² – 4ac formülünden;
Δ = 6² – 4.1.11
Δ = – 8 çıkan sonuç 0 dan küçük olduğu için kök yoktur.
b) x² – 13x – 3 = 0 denklemii için Δ = b² – 4ac formülünden;
Δ = (-13)² – 4.1.-3
Δ =169 + 12 = 181 yapar.
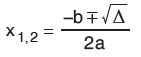formülünde değerleri yerine koyarsak;
x1,2 = (-(-13) ± √181)/2.1
x1,2 = (13 ± 9√2)/2 olarak buluruz.
c) 4 x² + 12 x + 9 = 0 denklemii için Δ = b² – 4ac formülünden;
Δ = 12² – 4.4.9
Δ = 144 – 144 = 0 olur. Bu durumda kökler eşittir. -b/2a formülünden;
x1 = x2 = -12/8 = -3/2 olarak buluruz.
Aşağıdaki yazılarımızdan da konu analtımı ve çözümlü soruları inceleyebilrisiniz
İkinci Dereceden Bir Bilinmeyenli Denklemler Konu Anlatımı
İkinci Dereceden Bir Bilinmeyenli Denklemler Çözümlü Sorular