DETERMİNANTLAR



MİNÖR VE KOFAKTÖR (EŞ ÇARPAN)
Tanım: n. sıradan bir A kare matrisinin i. Satır ve j. Sütun atıldıktan sonra geriye kalan matrisin determinantına, aij elemanının Minör’ü denir ve Mij ile gösterilir.
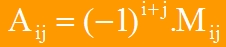
Tanım: 3×3 türünden bütün matrislerin kümesi M3 olsun.

DETERMİNANT FONKSİYONU
Tanım: n. Mertebeden kare matrislerin kümesi olsun.

DETERMİNANTLARIN ÖZELLİKLERİ
1) Bir kare matrisin, determinant değeriyle devriğinin determinant değeri eşittir.

2) Bir kare matrisin iki satır veya sütun elemanları orantılı ise, bu matrisin determinantının değeri sıfırdır.

determinantı verilmiş olsun. Bu determinantın birinci satırındaki terimlerle ikinci satırındaki terimler, karşılıklı olarak orantılı olduğu için, IAI=0 dır.
3) Bir kare matrisin herhangi bir satır veya sütununda buluna tüm terimler sıfır ise, determinantın değeri sıfırdır.

4) Bir kare matriste bir köşegenin üstündeki yada altındaki tüm elemanlar sıfır ise determinantın değeri köşegen üzerindeki elemanların çarpımı ya da bu çarpımın ters işaretlisine eşittir.

5) Bir determinantın iki satırı veya sütunu aralarında yer değiştirilirse, determinant işaret değiştirir.

6) Bir determinantın bir satır veya sütunu k sayısı ile çarpılırsa, determinantın değeri de k katına çıkar.

7) Bir determinantın herhangi bir satırında veya sütununda bulunan tüm terimlerin k katı alınarak, başka bir satırın veya sütunun elemanlarıyla toplanarak elde edilen yeni determinantın değeri değişmez.

8) Bir determinantın herhangi bir satırında veya sütunundaki her eleman iki terimin toplamından oluşuyorsa, bu determinant aynı sıradan iki determinantın toplamı biçiminde yazılabilir.

9. Bir determinantın herhangi bir satır yada sütunun ait terimler, bir başka satır veya sütunun terimlerine ait eş çarpanlar ile karşılıklı çarpılır ve çarpımlar toplanırsa, toplam sıfır olur.
3. Sıradan bir determinantta a11*A21+a12*A22+a13*A23 = 0 dır.
