10 Sınıf Matematik Fonksiyonlar İle İlgili Çözümlü Soruların ve Problemlerin olacağı bu yazımızda her bir sorunun detaylıca çözümlemesini yaptık.
Çözümlü sorular, sabit, birim, bileşke ve tek fonksiyondan olmak üzere karışık fonksiyon örneklerinden oluşmaktadır.
Soru: f:R→R,f(4)=5, f(x+2)=x.f(x)−3 olduğuna göre f(8) kaçtır?
Cevap: x yerine 4 koyarsak
f(6)=f(4+2)=4f(4)−3=4⋅5−3=17 olur.
Şimdi de x yerine 6 koyarsak
f(8)=f(6+2)=6f(6)−3=6⋅17−3=99 olarak buluruz.
Soru: f(x)=4+f(x−1) ve f(1)=3 ise f(15) kaçtır?
Cevap: f(x)=4+f(x−1)⇒f(x)−f(x−1)=4
x=2⇒f(2)−f(1)=4
x=3⇒f(3)−f(2)=4
x=4⇒f(4)−f(3)=4
⋮
x=15⇒f(15)−f(14)=4
f(15)−f(1)=14⋅4=56
f(15)=56+3=59

Soru: f doğrusal bir fonksiyondur.
f(x+3)+f(4x+5)=10x olduğuna göre, f(x) nedir?
Cevap: f(x) doğrusal ise f(x)=ax+b şeklinde olmalıdır.
f(x+3)=a(x+3)+b
=ax+3a+b
f(4x+5)=a(4x+5)+b
=4ax+5a+b
f(x+3)+f(4x+5)=10x
ax+3a+b+4ax+5a+b=10x
5ax+8a+2b=10x
5ax=10x
a=2
8a+2b=0
8⋅2+2b=0
b=−8
sonucuna ulaşırız. Böylece f(x)=2x−8 olur.
Soru: A = { – 1, 0, 1 } ve B = { 1, 2, 3 } kümeleri için A dan B ye tanımlı aşağıdaki
ilişkilerden hangileri bir fonksiyondur?
a. f = { ( – 1, 0 ), ( 0, 1) , ( 1, 2 ) }
b. k = { ( – 1, 3 ), ( 0, 3) , ( 1, 3 ) }
c. h = { ( – 1, 1 ), ( 1, 2) , ( 0, 2 ) }
d. p = { ( 0, 1 ), ( 1, 3) , ( – 1, 1 ) , ( 0, 2 ) }
e. g = { ( 0, 2 ), ( 1, 3) }
Cevap: b ve c seçenekleri birer fonksiyondur arkadaşlar. Detaylıca çözümü aşağıda görebilirsiniz.

Soru: Aşağıda şema ile gösterilen ilişkilerden hangileri bir fonksiyondur?

Cevap: a, b ve d seçenekleri birer fonksiyondur arkadaşlar, c seçeneği ise fonkiyon değildir, Çünkü c seçeneğindeki 2 rakamı herhangi bir şeyle eşleşmemiş.
Soru: Tanım kümesi A = { – 2, – 1, 0, 1 } olan bir f fonksiyonunun kuralı
f ( x ) = 1 – x 2 dir. Buna göre,
a. f fonksiyonunu sıralı ikililer şeklinde yazınız.
b. f ( A ) görüntü kümesini yazınız.
Cevap: İlk önce tüm f(x) fonksiyonlarını A kümesine göre yazalım
f ( -2 ) = 1 – (-2) 2 = 1-4= -3 olur.
f ( -1 ) = 1 – (-1) 2 = 1-1=0 olur.
f ( 0 ) = 1 – 0 2 = 1-0=1 olur.
f ( 1 ) = 1 – 1 2 = 1-1=0 olur.
Yukarıda bulmuş olduğumuz -3, 0 ve 1 değerleri sonuçlar kümesidir.
a. f fonksiyonunu sıralı ikililer şeklinde yazınız.
f= {(-2,-3), (-1,0), (0,1), (1,0)} olarak yazabiliriz.
b. f ( A ) görüntü kümesini yazınız.
f(A) = {-3,0,1} olur. (Aynı zamanda sonuçlar kümesidir.)
Soru: f = { ( 1, 3 ), ( 2, 3 ), ( a, 1 ), ( c, 2 ), ( d, – 1 ) } ifadesi bir fonksiyon belirtmektedir. Buna göre,
a. Fonksiyonun tanım kümesini yazınız.
b. Fonksiyonun görüntü kümesini yazınız.
Cevap: 
a. Fonksiyonun tanım kümesini yazınız.
Fonksiyonun tanım kümesi fonksiyonun ilk elemanlarıdır. Yani
A = {1,2,a,c,d} olur.
b. Fonksiyonun görüntü kümesini yazınız.
Görüntü kümesi de fonksiyonun 2. elemanlarıdır. Yani
f(A) = {3,1,2,-1} olur.
Soru: Tanım kümesi A, görüntü kümesi de B olan aşağıdaki fonksiyonlar için B = { – 1, 3, 4 } olduğuna göre her bir fonksiyon için A kümesini bulunuz.
a. f ( x ) = x + 2
b. k ( x ) = (x + 1)/3
c. h ( x ) = 1/(x + 1)
d. p ( x ) = (x + 1)/(x-1)
Cevap: a seçeneği için
x+2=-1 den x=-3 olur
x+2=3 ten x=1 olur
x+2=4 ten x=2 olur
A = {1,2-3} olarak cevabı buluruz.
b seçeneği için
(x+1)/3 = -1 den x = -4 olur
(x+1)/3 = 3 den x = 8 olur
(x+1)/3 = 4 den x = 11 olur
A = {-4, 8, 11} olarak cevabı buluruz.
c seçeneği için
1/(1+x) = -1 den x = -2 olur.
1/(1+x) = 3 den x = -2/3 olur.
1/(1+x) = 4 den x = -3/4 olur.
A = {-2, -2/3, -3/4} olarak cevabı buluruz.
d seçeneği için ise
(x+1)/(x-1) = -1 den x = 0 olur.
(x+1)/(x-1) = 3 den x = 2 olur.
(x+1)/(x-1) = 4 den x = 5/3 olur.
A = {0, 2, 5/3} olarak cevabı buluruz.
Soru: Aşağıdaki fonksiyonların her biri için f ( – 1 ), f ( 0 ) ve f ( 2 ) değerlerini bulunuz.

Cevap: Tüm şıkların cevaplarını aşağıda bulabilirsiniz arkadaşlar.


Soru: Gerçek sayılarda tanımlı f ( x ) = 2x – 1 ve h ( x ) = 4 – 3x fonksiyonları için,
a. f ( a ) = h ( a ) ise a kaçtır?
b. f ( 2b ) = h ( – b ) ise b kaçtır?
Cevap: a şıkkı için
2a -1 = 4 -3a
5a=5
a=1 olarak buluruz.
b şıkkı için ise
2.2b -1 = 4 -3.(-b)
4b -1 = 4 + 3b
b= 5 olarak buluruz.
Soru: Aşağıdaki fonksiyonların tanım kümelerini bulunuz.

Cevap: Tüm cevapları aşağıda bulabilirsiniz arkadaşlar.

Soru: Aşağıdaki f fonksiyonları birim fonksiyonlardır. Buna göre her bir seçenekteki m ve n sayılarını bulunuz.

Cevap: Tüm cevapları aşağıda bulabilirsiniz arkadaşlar.

Soru: Aşağıdaki g fonksiyonları sabit fonksiyonlardır. Buna göre her bir seçenekteki g ( m ) değerlerini bulunuz.
a. g ( x ) = ( m + 2 ) x + m + 1
b. g ( x ) = 4x – ( m + 1 ) x – m
c. g ( x ) = ( m + 3 ) x + 5
Cevap: Sabit fonksiyon olduğuna göre x terimli bir ifade olmamalı. Bu nedenle de x terimlerini yok etmemiz için başlarındaki katsayıyı 0 yapmalıyız.
a şıkkındaki g ( x ) = ( m + 2 ) x + m + 1 fonksiyonunda ( m + 2 ) buranın 0 a eşit olması gerek. Bu nedenle de m=-2 olur.
m yerine -2 değerini koyarsakta g(-2) = ( -2 + 2 ) x – 2 + 1 = -1 olarak buluruz.
b şıkkında ise g ( x ) = 4x – ( m + 1 ) x – m fonksiyonunda 4 -m -1 = 0 olmalı
Buradan da m = 3 oalrak buluruz.
m değerini yerine koyarsak g(x) = – m den g(3) = -3 olur.
c şıkkında ise g ( x ) = ( m + 3 ) x + 5 fonksiyonunda (m + 3) = 0 olmalı ve buradan da m = -3 olur.
m değerini yerine koyarsak g(x) = 5, g(-3) = 5 olarak buluruz.
Soru: Birikmiş 100 TL parasından her gün 5 TL para harcayan Bülent’in günlere ( x ) göre kalan parasını ( y ) veren y = f ( x ) fonksiyonunu bulup tanım ve görüntü kümelerini belirleyip grafiğini çiziniz.
Cevap: y=f(x) = 100 – 5x olur.
x: gün
x = 0 için y = 100
x = 1 için y = 95
.
.
.
x = 20 için y = 0
f : [0,20] buradan da [0,100] olur
Grafiğini çizecek olursak ta

Soru: Dikildiğinde 20 cm boyunda olan bir fidan her ay 2 cm uzamaktadır. Fidanın aylara ( x ) göre boyunu ( y ) veren y = f ( x ) fonksiyonunu bulup tanım ve görüntü kümelerini belirtip grafiğini çiziniz.
Cevap: Yanıtı aşağıdaki grafik ve açıklamalarda bulabilirsiniz arkadaşlar.

Soru: f ( x ) doğrusal fonksiyonunda f ( 2 ) = 5 ve f ( – 1 ) = – 1 olduğuna göre f ( 5 ) kaçtır?
Cevap: f(2) = 5 ise 2.2 + 1 = 5 şeklinde olabilir
f(-1) = -1 ise 2.(-1) + 1 = -1 olabilir
Yukarıdaki her iki fonksiyonda görüleceği üzere
f(x) fonksiyonumuz 2x + 1 olur. O halde
f(5) = 2.5 + 1 = 11 olur.
Soru: f : R→ R, f ( x ) = ( 2a – 4 )x 3+ ( b + 4 )x 2+ ( 4b – 8 ) x – 3a – b + 1 fonksiyonu çift fonksiyondur. Buna göre f ( 1 ) in değerini bulunuz.
Cevap: Çift fonksiyon olduğuna göre tek dereceli terimler olmamalı arkadaşlar.
Bu nedenle de;
2a – 4 = 0 dan a = 2
4b – 8 = 0 dan b=2 olur.
f(x) = 6x 2 – 7 den
f(1) = 6-7= -1 olarak buluruz.
Soru: Gerçek sayılarda tanımlı f ve h fonksiyonları için
f ( x ) = – x + 5 ve
( 3h – f ) ( x ) = 10 x – 2
olduğuna göre h ( 3 ) aşağıdakilerden hangisidir?
Cevap: f(x) fonksiyonunda f(3) = -3 + 5 = 2 olur.
(3h-f).(x) = 3.h(x) – f(x) = 10x -2 olur
x=3 için 3.h(3) – f(3) = 10.3 -2
3.h(3) – 2 = 28
3.h(3) = 30
h(3) =10 olarak buluruz.
Soru: Gerçek sayılarda tanımlı f ve h fonksiyonları için
f ( x ) = – x + 5 ve
( 3h – f ) ( x ) = 10 x – 2
olduğuna göre h ( 3 ) aşağıdakilerden hangisidir?
Cevap: f(x) fonksiyonunda f(3) = -3 + 5 = 2 olur.
(3h-f).(x) = 3.h(x) – f(x) = 10x -2 olur
x=3 için 3.h(3) – f(3) = 10.3 -2
3.h(3) – 2 = 28
3.h(3) = 30
h(3) =10 olarak buluruz.

Soru: Yukarıda verilen y = f ( x ) fonksiyonunun grafiğine göre,
a. f ( – 5 ) , f ( – 3 ) , f ( – 2 ) , f ( 1 ) ve f ( 4 ) değerlerini bulunuz.
b. f ( a ) = 0 olmasını sağlayan kaç a ∈ R sayısı vardır?
Cevap: a şıkkı için;
(-5,8), (-2,2), (-3,-1), (1,1), (4,0) f(x) üzerinde olduğu için
f(-5) = 2
f(-2) = 2
f(-3) = -1
f(1) = 1
f(4) = 0 olur.
b şıkkı için ise ;
f(a)= 0 sonucu olan noktaları a ya eşitleyelim.
f(-4) = 0 a=-4
f(m) = 0 a=m
f(4) = 0 a=4
O halde 3 farklı a ∈ R sayısı vardır.
Soru: A = { 1, 2, 3 } , B = { –1, 0, 1 } ve C = { 6, 7, 8 } kümeleri veriliyor. f : A → B ve g : B → C olmak üzere “ 95.Şekil ” de gösterilen f ve g fonksiyonları doğrusaldır. Buna göre,

a. f ve g fonksiyonlarının kurallarını bulunuz.
b. g o f fonksiyonunun kuralını bulunuz.
c. ( g o f ) ( 2 ) ve ( g o f ) ( 3 ) değerleri kaçtır?
d. ( g o f ) ( a ) = 6 ise a kaçtır?
Cevap: Şıkları sırasıyla cevaplaaycak olursak
a. f ve g fonksiyonlarının kurallarını bulunuz.
f(x) = x-2 g(x) = x+7 olur.
b. g o f fonksiyonunun kuralını bulunuz.
(gof)(x)= x-2+7 = x + 5 olur.
c. ( g o f ) ( 2 ) ve ( g o f ) ( 3 ) değerleri kaçtır?
g(f(2)) = g(0) = 7 (gof)(3) = g(f(3)) = g(1) = 8 olur.
d. ( g o f ) ( a ) = 6 ise a kaçtır?
g(f(a)) = 6 f(a) = -1 den a = 1 olur.
Soru: Gerçek sayılarda tanımlanan f ( x ) = 2 x – 3 , g ( x ) = 1 – x ve h ( x ) = 3x + 1 fonksiyonlarını kullanarak aşağıdaki fonksiyonların kurallarını bulunuz.
a. ( f o g ) ( x ) b. ( g o f ) ( x )
c. ( g o h ) ( x ) d. ( h o g ) ( x )
e. ( f o h ) ( x ) f. ( h o f ) ( x )
Cevap: a. ( f o g ) ( x ) için
2.(1-x) -3 olur ve buradan da -2x -1 olarak buluruz
b. ( g o f ) ( x ) için
1-(2x-3) bu da 1-2x +3 = 4 -2x olur.
c. ( g o h ) ( x ) için
1- (3x +1) = -3x olur.
d. ( h o g ) ( x ) için;
3.(1-x) + 1 = -3x + 4 olur.
e. ( f o h ) ( x ) için
2.(3x + 1) -3 = 6x -1 olur.
f. ( h o f ) ( x ) için
3.(2x-3) +1 = 6x-8 olur.
Soru: Gerçek sayılar kümesinde tanımlı f ve g fonksiyonları için f ( x ) = 3x – 1 ve (gof) ( x ) = 2 x + 5 olduğuna göre g(x) i bulunuz.
Cevap: g(f(x)) = 2x + 5
g(3x-1) = 2x + 5
g(x) = 2.(x+1)/3 + 5
g(x) = (2x+2)/3 + 5
g(x) = (2x+17)/3 olur.
Soru: Gerçek sayılar kümesinde tanımlı f ( x ) = 5 – 2 x ve g ( x ) = 3 x + 1 fonksiyonları veriliyor. Buna göre,
a. ( f o g ) ( 2 ) kaçtır? b. ( g o f ) ( 2 ) kaçtır?
Cevap: a. ( f o g ) ( 2 ) için
( f o g ) ( 2 ) = f(g(2)) buradan g(2) = 3.2 + 1 = 7 olur
=f(7)
=5 – 2.7
=5-14
= -9 olur.
b. ( g o f ) ( 2 ) için
= g(f(2)) buradan f(2) = 5-2.2 olur ve f(2)=1 olur.
= g(1)
=3.1 + 1
= 4 olarak buluruz.
Soru: Gerçek sayılarda tanımlı f fonksiyonu için f ( x ) = 3 – 2 x ve ( f o f ) ( a ) = 8 olduğuna göre a kaçtır?
Cevap: f(f(x)) = 3 – 2.(3-2x)
(fof)(x) = 3 -6 + 4x = 4x-3
(fof)(a) = 4a-3=8
4a = 11
a= 11/4 olarak buluruz.
Soru: f ( x ) = | x – 3 | + 4 ve h ( x ) = x 3 – x + 1 fonksiyonu için f ( 1 ) ve h ( – 1 ) değerlerini bulunuz.
Cevap: f(1) = |1-3| + 4 = 2+4 = 6 olur.
h(-1) = (-1)3 – (-1) + 1 = -1 + 1 + 1 = 1 olur.
Soru: Aşağıdaki fonksiyonların tanım kümelerini bulunuz.
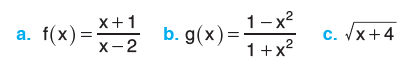
Cevap: Tüm şıkların tanım kümelerini aşağıda bulabilirsiniz.

Soru: f : R ” R , f ( x ) = ( k + 2 ) . x – m + 4 fonksiyonu birim fonksiyondur. Buna göre f ( m + k ) kaçtır?
Cevap: f(x) birim fonksiyon olduğuna göre f(x) = x olur.
k+2=1 den k = -1
-m + 4 = 0 dan m = 4 olur.
m + k = 3 yapar.
f(m+k) = m+k dan f(3) = 3 olarak sonucu buluruz.
Soru: f ( x ) = ( a – 3 ) x + 4 fonksiyonu sabit fonksiyon olduğuna göre f ( a ) kaçtır?
Cevap:Sabit fonksiyon olduğuna göre x li terim olmaması gerek.
f(x) = 0.x + k
a – 3 = 0
a=3 olarak buluruz.
f(x) = 4 ten
f(3) = 4 oalrak sonucu bulmuş oluruz.
Soru: f : R ” R , f bir doğrusal fonksiyondur. f ( 1 ) = 4 ve f ( – 2 ) = – 2 olduğuna göre f ( 3 ) kaçtır?
Cevap: Çözümü aşağıda bulabilirsiniz arkadaşlar.

Soru: f ( x ) fonksiyonunun grafiği y eksenine göre simetriktir. f ( –x ) + 4x 4 = 6 x 2 – f ( x ) + 2 olduğuna göre f ( –1 ) kaçtır?
Cevap: Çözümü aşağıda bulabilirsiniz arkadaşlar.

Soru: f ( x ) = ( 4a – 8 ) x 5 – ( 3b + 12 ) x 2 + a – 6 fonksiyonu tek fonksiyon ise a + b toplamı kaçtır?
Cevap: f fonkiyonu tek fonksiyon olduğuna göre çift kuvetlerin katsayıları 0 olur.
3b + 12 = 0 dan b = -4 olur.
a-6 = 0 dan a = 6 olur.
a + b = 6 -4 = 2 olarak buluruz.
Soru: R de tanımlı, f ve g fonksiyonları için,
f ( x ) = 2 – x ve
( 2g – f ) ( x ) = 5 x – 2
olduğuna göre g ( 2 ) aşağıdakilerden hangisidir?
Cevap: 2.g(x) – f(x) = 5x -2
2.g(x) + x -2 = 5x – 2
2.g(x) = 4x
g(x) = 2x
g(2) = 4 olarak sonucu bulmuş oluruz.
Soru: R de tanımlı, f ve h fonksiyonları için,
f ( x ) = 3 x + 1 ve
h ( x ) = x 2 – 1
olduğuna göre ( foh ) ( –1 ) değeri kaçtır?
Cevap: ( foh ) ( –1 ) = f(h(-1)) buradan h(-1) = -1 üzeri 2 -1 = 0 olur.
= f(0)
=1 olarak sonucu buluruz.
Soru: 
Soru: 
Soru: R de tanımlı, f ve k fonksiyonları için,
( x ) = 3x – 1 ve
( fok ) ( x ) = 4x + 5
olduğuna göre k ( x ) i bulunuz.
Cevap: f(k(x)) = 4x + 5
3.k(x) -1 = 4x + 5
3.k(x) = 4x + 6
k(x) = (4x + 6)/3 olur.
Soru: 
Soru: 
Soru: 
Soru: 