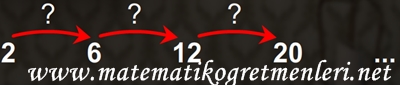
Elimizde 2 -6 – 12 – 20 ….. olarak devam eden bir sayı örüntüsü olsun.

Şimdi bu sayı örüntüsündeki ilişkiyi bulmaya çalışalım. İlk bakışta bu sayı örüntüsündeki sayılar arasında nasıl bir ilişki olduğunu görmekte zorlanabiliriz.
Şimdi bu ilişkiyi anlayabilmek için bir model oluşturmaya çalışalım.
Sayı örüntüsünün ilk sayısı olan 2 sayısı için 2 adet birim küp kullanalım ve bir dikdörtgenler prizması elde edelim.

Örüntüdeki diğer rakamlar için de aynı işlemi yapalım.
6 sayısı için 6 adet küp, 12 sayısı için 12 adet küp, 20 sayısı için 20 adet küp kullarak daha büyük dikdörtgenler prizması oluşturalım.

Şimdi sayı örüntümüzü model üzerinden somutlaştırdık ve daha açık biçimde görebiliyoruz. Bu modelden farklı olarak daha değişik modeller de oluşturabiliriz.
Şimdi de modelimizdeki sıra numaralarını ve küp sayılarını bir tabloya aktaralım.

Yukarıdaki tabloda gördüğünüz gibi, 1 sıra için 2 adet küp, 2. sıra için 6 adet küp, 3. sıra için 12 adet küp, 4. sıra içinse 20 adet küp kullanıldı. Bizlere verilen sayılar dışında … ile gösterilen örüntünün dışındaki sayıları göremiyoruz. Bu sebeple örüntüdeki sayıların sayısını veya yerini belirtmek için bir sembol olarak n harfini kullanabiliriz. Matematikte bu n harfine örüntünün temsilci sayısı, n inci sayısı ve ya genel sayısı denir.

Tabloyu dikkatlice incelediğimizde birinci sıra sayısıyla bu sıra sayısının bir fazlasının çarpımının kullanılan küp sayısına eşit olduğunu görüyoruz.
Aynı işlem diğer sayılar için de geçerlidir.
Bu sonuçtan çıkarımla bir genelleme yaparak temsilci sayı, n sayısını kullanarak n(n+1) şeklindeki bir ilişkiye ulaşabiliriz. Bu ilişkiyi de sayının örüntüdeki sıra numarasıyla bir fazlasının çarpımı şeklinde söyleyebiliriz. Ayrıca bu sayı örüntüsü farklı şekillerde de ifade edilebilir.

Yukarıdaki tabloya dikkat ettiğimizde her bir sayı için kullanılan küp sayısının sayının karesiyle örüntüdeki küp sayısının toplamına eşit olduğunu görürüz. Dolayısıyla bu sayı örüntüsünü nkare + n olarak yazabileceğimiz gibi sayının karesi ile sıra numarasının toplamı şeklinde söyleyebiliriz.
Bu sayı örüntüsündeki ilişkilerde n nin yerine herhangi bir doğal sayıyı koyarak örüntüde bu doğal sayıya denk gelen sayıyı bulabiliriz.
Örnek:
Örüntüdeki 10. Sayıyı bulalım.

İlişkideki n nin yerine 10 yazarız ve 10uncu sayıyı 110 olarak buluruz.

bu konu anlatımı vitamin videoları kaynak alınarak hazırlanmıştır.